In Exercise 12 from the “Basics of C++” worksheet, we wrote a C++ program to compute the area of a triangle given the lengths of its three sides a, b and c, according to the equation
\[A = s(s − a)(s − b)(s − c)\]where s is half of the sum of the three sides. However, this equation can only be used if the values of a, b and c represent a valid triangle. This is true if, for each of the three sides, its length is less than the sum of the lengths of the two remaining sides.
Modify your solution to that previous exercise so that it first checks if the numbers entered represent a valid triangle. If they do, the program should compute and display the area of that triangle. If they do not then throw an exception with the message “Not a valid triangle”.
The equation for computing a person’s body mass index (BMI) is:
\[\textrm{BMI} = \textrm{mass} \times \textrm{height}^2\]where the mass is in kilograms and the height is in metres. A BMI of less than 18.5 is classified as underweight, between 18.5 and 25 is normal, between 25 and 30 is overweight and more than 30 is obese.
Write a C++ program that takes the mass and height of the user as input (whether as command-line arguments or through the terminal), computes their BMI and then display their classification according to the rules described above.
In exercise 11 of “Basics of C++” worksheet, we debugged a C++ program to compute the roots of a quadratic equation of the form:
\[ax^2 + bx + c = 0\]The formula for solving for x is:
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]However, this equation is only valid if the roots are real, i.e. if b2 ≥ 4ac.
Modify your solution to the previous exercise so that after reading the values of a, b and c it first checks to see if the roots of the equation are real. If they are, it computes and displays the roots. Otherwise it displays a message informing the user that the roots are imaginary.
Write a C++ program that calculates and prints out all of the prime numbers between 1 and 50.
Modify your solution to Exercise 1 so that, after computing the area of a triangle, the program asks the user if they want to compute another area. The user should enter either ‘y’/‘Y’ or ‘n’/‘N’. Based on this answer the program should either exit or prompt the user to enter values for a, b and c again. The program should compute the area of one triangle before asking the user if they want to proceed.
The Fibonacci series is a sequence of integer numbers, starting with 0 & 1, such that each subsequent number in the sequence is equal to the sum of the previous two. For example, the beginning of the sequence is 0, 1, 1, 2, 3, 5, 8, 13, etc. Write a C++ program that computes and prints the Fibonacci series up to a maximum value of 10000 (i.e. when the sum of the previous two numbers is greater than 10000 the program should stop).
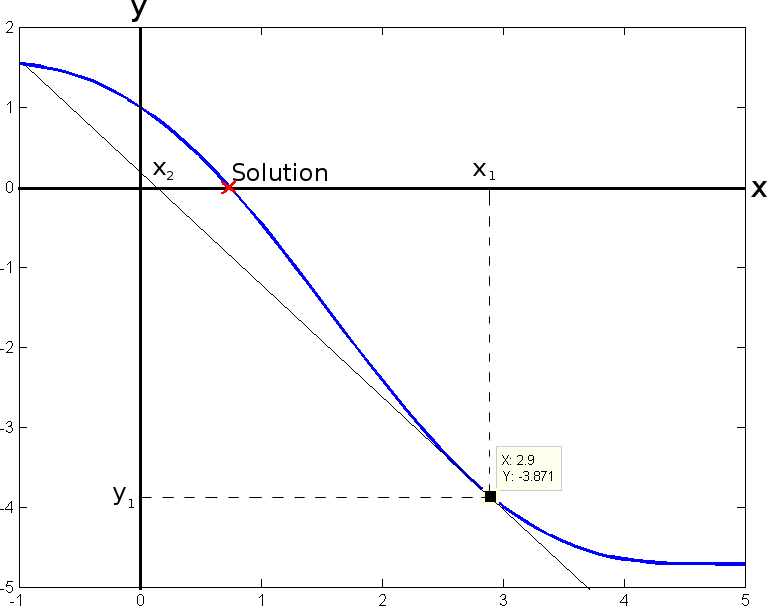
In numerical analysis, the Newton-Raphson method is a method for successively finding better approximations of the root(s) of a function. To approximate the unknown value of x that satisfies the equation f(x) = 0, the method works as follows (see figure below):

This sequence of steps should continue until some convergence condition, e.g. (xn − xn−1) < ϵ.
Write a C++ program to find the root of the equation f(x) = cos(x)−x using the Newton-Raphson method with ϵ = 0.001 (The derivative of cos(x) − x is −sin(x) − 1.)
Write a C++ program that reads in a sequence of positive integers from the keyboard. When a negative number is entered the program should stop reading numbers and output the sum, range (i.e. maximum minus minimum) and mean of the positive integers.
Hint: the <limits> header include file defines functionality to
query the minimum and maximum values
for all the generic data types, for example:
const int int_min = std::numeric_limits<int>::min();
const int int_max = std::numeric_limits<int>::max();
You can use these to initialise your minimum and maximum values.
Write an interactive C++ program that successively reads a floating point number from the keyboard followed by an integer code. If the code entered is a 1 the program should display the sine of the floating point number. If it is a 2 it should display the cosine, and if it is a 3 it should display the tangent. The program should terminate when the code entered is −1. If a code other than 1, 2, 3 or −1 is entered the program should inform the user and ask them to re-enter the numbers. Use a switch statement in your solution.
In the 18th century Leonard Euler showed that:
\[\sum_{n=1}^N \frac{1}{n^2}\]converges to π2/6 for very large N.
Write a program that estimates the value of π using this approximation, and finds the value of N for which the error in the approximation becomes less than 0.001.